所感
総評:取り組みやすい問題が多いが,解答数が多い。
答えるものの数は多いものの,系としては取り組みやすいセットです。取るべき問題をしっかりと取っていけば30点は目指せるでしょう。
2020年全体の特徴
- 系としては取り組みやすい。
- 解答する答えの数が多い。
- 頭を使って考える問題が少ない。
出題量について
全体として問題数が多いセットです。解答するものの数は「42個」でした。
それに伴い,1問あたりの配点は少なくなります。それゆえ,答えを確実に合わせることが重要なセットといえるでしょう。
前半部分の平易な問題は答えのみ,後半の難しめの問題は答えに自信があれば最小限の記述で解答,自信がなければ丁寧に途中経過を記述して部分点を狙いにいく,という策略になるかと思います。
内容について
どの設問も取り組みやすい系だったように思います。
真新しい系は少なく,似たテーマの問題には触れたことがあったのではないでしょうか。
解く順番
問題量はどれもそこそこ。図を見ると,第2問がよくある「棒が動くタイプの問題」であることがわかるので,第2問から取り組むと良いでしょう。
第1問,第3問は好みによって分かれると思いますが,第3問の熱力学は問題文の図と $P-V$ グラフをみる限り,断熱変化や定圧変化を繰り返す状態変化の問題であることが予想できるため,こちらから先に解くのが良いでしょうか。
推奨解答順序
第2問 → 第3問 → 第1問
上記を推奨としますが,「絶対に最初に解くべき問題」「絶対に最後に回すべき問題」はないので,どの順番で解いても大きな差はないでしょう。
第1問:面積速度保存則の理解を問う問題。
前半は面積速度保存則の問題であり,「物体に中心力のみが作用するとき,面積速度が保存する」ことを理解できていればスラスラと解き進められたはず。
一方で,面積速度保存則を「ケプラーの第二法則」として捉えていて,「惑星の問題で使うもの」と認識している場合には難しく感じたのではないかと思います。
入試本番では,Ⅱの扱いが重要で得点を大きく左右したはず。(1)は式変形の見通しが立てば時間がかからないですが,(2)は考え始めると泥沼化する問題。
こういった問題は 一旦飛ばして後で戻ってこれたら戻ってくる という戦略をスムーズに取ることが非常に重要。
Ⅲについては基本的な問題であり,確実に得点したいところです。(2)は時間と心に余裕がなければ一旦飛ばしても良いでしょう。
第2問:動く棒のオーソドックスな問題。差がつきやすい。
非常にオーソドックスな系であり,差が付きやすい問題。
動く棒の問題に慣れていれば,「はいはい,いつものやつね!」と自信を持って解き進められたはず。
一部難しい設問もありますが,10点は割らないでしょう。
一方で,動く棒の問題に慣れていないと大崩れする可能性もあるでしょう。
こうしたオーソドックスな問題で大失敗すると致命的になりかねないため,最低限の得点はしっかり取りたいところです。
内容として差がつくのは Ⅰ(3),Ⅱ でしょう。
第3問:状態変化の組み合わせ。状況をどこまで整理できるかで差がつく。
断熱変化,定圧変化の内容ですが,ポアソンの法則を利用することはなく,各状態での温度,圧力,体積が表で与えられています。
定圧変化の性質をうまく使える問題もありますが,全体としては系のエネルギー保存を正しく捉えられるかに尽きるでしょう。
この手の「複数の気体をまとめて1つの系とみなして,エネルギー収支を考える」タイプの問題は頻出であり,非常に差が付きやすいので類題の演習を通じてしっかりと理解しておく必要があります。
状態変化の全体像を試験時間内に正しく理解し切るのはかなり難しいと思いますが,各設問設問ではしっかりと誘導が与えられているので,必要な情報をしっかりと読み取って式を立てていければ,高得点も十分期待できます。
「何が起こっているか」までしっかりと理解できれば,短時間で満点を取ることも可能でしょう。
目標点
| 科類 | 第1問 | 第2問 | 第3問 | 計 |
|---|---|---|---|---|
| 理Ⅰ・Ⅱ | 13点 | 11点 | 12点 | 36点 |
| 理Ⅲ | 17点 | 15点 | 16点 | 48点 |
参考資料
東京大学公式ホームページは以下です。

解答の作成方法など,東大物理の対策総論については以下のページもご参考に。
こちらもCHECK
-

-
東京大学 物理 傾向と対策
東大物理の傾向分析のページです。
試験時間の使い方や解答作成方法について,詳しく説明しています。続きを見る
難易度・配点
第1問
| 設問 | 難易度(A〜D) | 配点 | |
|---|---|---|---|
| Ⅰ | (1) | A | 6点 |
| (2) | A | 2点 | |
| (3) | B | 2点 | |
| Ⅱ | (1) | C | 2点 |
| (2) | D | 3点 | |
| Ⅲ | (1) | A | 3点 |
| (2) | B | 2点 | |
第2問
| 設問 | 難易度(A〜D) | 配点 | |
|---|---|---|---|
| Ⅰ | (1) | A | 5点 |
| (2) | B | 2点 | |
| (3) | C | 2点 | |
| (4) | D | 2点 | |
| (5) | B | 2点 | |
| Ⅱ | B | 4点 | |
| Ⅲ | C | 3点 | |
第3問
| 設問 | 難易度(A〜D) | 配点 | |
|---|---|---|---|
| Ⅰ | A | 6点 | |
| Ⅱ | (1) | B | 2点 |
| (2) | B | 2点 | |
| (3) | C | 2点 | |
| Ⅲ | (1) | B | 2点 |
| (2) | C | 2点 | |
| (3) | D | 2点 | |
| (4) | D | 2点 | |
採点基準
第1問
| 設問 | 基準 | 点数 | |
|---|---|---|---|
| Ⅰ | (1) | 空欄に入る数式を答えて | 各1点 |
| (2) | 運動方程式に言及して | 1点 | |
| 正しく説明を終えて | 1点 | ||
| (3) | 仕事が等しくなると述べて | 1点 | |
| 正しく理由を説明して | 1点 | ||
| Ⅱ | (1) | 正答を得て | 2点 |
| (2) | 運動エネルギーを分解して | 1点 | |
| 力学的エネルギーの最小値を答えて | 1点 | ||
| 運動を正しく述べて | 1点 | ||
| Ⅲ | (1) | 運動方程式を立式して | 1点 |
| 正答を得て | 1点 | ||
| (2) | 正答を得て | 2点 | |
第2問
| 設問 | 基準 | 点数 | |
|---|---|---|---|
| Ⅰ | (1) | 空欄に入る数式を答えて | 各1点 |
| (2) | $\varDelta s$ を求めて | 1点 | |
| $\varDelta V$ を求めて | 1点 | ||
| (3) | 方針を正しく示して | 1点 | |
| $Q$ を求めて | 1点 | ||
| (4) | $W=1/2\,QV_0$ を述べて | 1点 | |
| 仕事を求めて | 1点 | ||
| (5) | エネルギーの種類と量を求めて | 各1点 | |
| Ⅱ | 空欄に入る数式を答えて | 各1点 | |
| Ⅲ | 到達速さの比を述べて | 1点 | |
| 到達速さを求めて | 各1点 | ||
第3問
| 設問 | 基準 | 点数 | |
|---|---|---|---|
| Ⅰ | $W_1\,,\,W_2\,,\,W_3$ を求めて | 各2点 | |
| Ⅱ | (1) | 正答を得て | 2点 |
| (2) | 定圧変化であることを述べて | 1点 | |
| 正答を得て | 1点 | ||
| (3) | エネルギー保存則を立式して | 1点 | |
| 正答を得て | 1点 | ||
| Ⅲ | (1) | 正答を得て | 2点 |
| (2) | 条件を正しく述べて | 1点 | |
| 正答を得て | 1点 | ||
| (3) | 容器X内の気体の内部エネルギー変化を求めて | 1点 | |
| 正答を得て | 1点 | ||
| (4) | 条件を正しく述べて | 1点 | |
| 正答を得て | 1点 | ||
第1問
手書き解答
東大2020_1Ⅱ(1)について
計算問題であり,途中過程に部分点がない可能性も高いため,時間によっては答えのみでも可と思われる。
Ⅱ(2)について
Ⅱ(1)を利用して,運動エネルギーを分解する過程は書いておきたいところ。
Ⅲ(2)について
最後の問題で配点も低い可能性が高い。数値計算問題であり,途中点がない可能性も高いため,答えのみ記述した。
Ⅰ(1)
まぁ流石に,という穴埋め問題。
面積速度の見慣れない式が出てきますが,深く考えずに誘導に従って解いていけばokでしょう。
なお,問題文の「なお,$(\varDelta t)^2$ に比例した面積速度の変化分は無視する」とありますが,物理で扱う微小量については基本的に「微小量の2乗は無視」です。これはルールとして押さえておくべきです。
Ⅰ(2)
言い換えると,「面積速度が保存される条件を求めよ」という問題です。
「中心力のみが働くとき,面積速度が保存される」 ことを知っていればもはや,という設問。
面積速度 $A_v$ の中には $a_x$ ,$a_y$ という加速度が含まれていて,設問では $F_x$ ,$F_y$ という力の条件を求められているわけですから,これらを結びつけるために運動方程式を使う,とスムーズに考えたいところ。
Ⅰ(3)
面積速度が保存される状況下では,合力が中心力となるはずです。
物体の運動は円運動で,速度は接線方向となるわけですから,$\vec{F}\perp\vec{v}$ ですよね。
あとはこれをまとめて記述すればok。
Ⅱ(1)
計算問題です。
$$\begin{aligned}\left\{\begin{array}{l}r^2&=x^2+y^2\\v^2&=v_x\!^2+v_y\!^2\end{array}\right.\end{aligned}$$
を使ってひたすら式変形をしていきます。
ただし,答えで使える文字は $m$ ,$r$ ,$A_v$ ですので,$$A_v\!^2=\bun14(xv_y-yv_x)^2$$の形を作るんだろうな,という見通しが立ちます。 $$\bun12mv^2-\bun12mv_r\!^2$$の引き算の形から $(xv_y-yv_x)^2$ をうまく作り出せるように変形を進められると良いでしょう。
盲目的に計算するのではなく,答えの形から「この形がでてくるはず」「こんな式変形の過程になるはず」という見通しを予め立てることが大事です。
Ⅱ(2)
(1)が誘導になっていることは容易に想像できるので,$$E=\bun12mv_r\!^2+\bun{2mA_0\!^2}{r^2}-G\bun{mM}{r}$$という変形まではスムーズに行いたいところ。
ここからは最大・最小問題になるわけですが,戸惑った人も多いでしょう。
この手の問題は泥沼化するので,3分くらい考えて見通しが立たなければ一旦飛ばすのが吉。特に今回はⅢに影響しない内容で,Ⅲが得点しやすい内容ですのでこの戦略が特に重要。
「Ⅱ(2)に時間を取られすぎてⅢに目を通さず,Ⅲ(1)で失点しまった…」という人は大反省です。
しかしながら,飛ばすにしても「どうせ等速円運動だろう」という予測は立ちますよね。計算はできなくても,「等速円運動のとき」とだけ書いておいて,部分点はしっかりもらっておきたいところ。
なお,「等速円運動だろう」という予測から解き進めることも可能です。等速円運動であれば $r$ が一定になりますので,$v_r=0$ ですよね。これがわかれば,$$E=\bun{2mA_0\!^2}{r^2}-G\bun{mM}{r}$$となりますが,変数は $r$ だけですのでかなり見通しが良くなるでしょう。
Ⅲ(1)
原子物理の基本問題。Ⅱまでの内容とは独立しており,必ず得点したい問題です。
このように,後半に基本問題があることは多いため,「何があっても必ず全ての問題に目を通す」ことはとても重要です。

「後半だし,難しいだろう」という先入観で,本問に手を付けなかった人は大反省。
Ⅲ(2)
一見複雑そうに見えるものの,実は大したことのない計算問題。
ただし,ある程度計算してみないとどのくらいの計算量かわからないため,時間が厳しい場合はいったん飛ばしてしまってもよいでしょう。
可能であれば,値を代入するだけしてみて,どのくらいの計算量かをまず確認するのが良いでしょう。計算が楽そうであればそのまま計算して,複雑そうであればいったん飛ばす,という選択を取るのが理想です。
第2問
手書き解答
東大2020_2Ⅰ(2)について
運動方程式,誘導起電力を表す $V=dsB$ は記述しておく。
Ⅱ(3)について
$Q$ を求める式である $Q=\displaystyle\int I\dt$ は記述しておく。積分区間を含めると,$\displaystyle\int_{0}^{\infty}I\dt$ となってしまい,高校範囲を超えてしまうため,あえて積分区間は明示していない。
Ⅲについて
働く力が常に $2:1$ であるから,到達速さが $2:1$ になることを明記した。時間がなければ「到達速さの比が $2:1$ になるので〜」などと簡潔化するのも可。
Ⅰ(1)
よくある「棒が動くタイプ」の問題。
立てる式は基本的に「運動方程式」と「キルヒホッフの第二法則」の2つです。これに加えて,必要に応じてエネルギー保存則,という流れですね。
この時点で手が止まったら完全に負けです。まだまだ練習量が足りないと言わざるを得ない。
「十分時間が経ったら?」という回路の問題もお決まりで,「変化が起こらなくなる」というのがポイントです。
流れる電流は一定になり(そのため,振動回路でない限りコイルの電圧は $0$ ),コンデンサーに蓄えられる電化は一定になります(そのため,振動回路でなければコンデンサーに流れ込む電流は $0$ )。
Ⅰ(2)
(1)で運動方程式の議論をしていないので,棒の運動方程式を立てて $\varDelta s$ を求めるんだろうな,という着眼点は難しくないはず。
加速度を $\bun{\varDelta s}{\varDelta t}$ の形で立式すればスッキリしますね。
$\varDelta s$ が求められれば,$\varDelta V$ は難しくはないでしょう。

ここまでは「間違えたら差をつけられてしまう問題」です。オーソドックスな内容なので,時間をかけずにスラスラと答えを出したいところ。
Ⅰ(3)
求めるのは「合計の電気量」です。単位時間あたりに回路を流れる電気量が電流 $I$ ですので,これを足し合わせていくことになります。
式で表すと,$$Q=\int_{0}^{\infty}I\dt$$になるので,$I$ を求めよう,という流れになるわけです。
そこで前問の答えに注目すると,$$I=\bun{m}{B^2d^2}\cdot\bun{dV}{\dt}$$であることがわかります。これより,
$$\begin{aligned}Q=\int_{0}^{\infty}I\dt&=\int_{0}^{\infty}\bun{m}{B^2d^2}\cdot\bun{dV}{\dt}\dt\\&=\int_0^{V_0}\bun{m}{B^2d^2}dV\\&=\bun{m}{B^2d^2}\int_0^{V_0}dV\\&=\bun{mV_0}{B^2d^2}\end{aligned}$$
と計算できます。
途中で積分変数が $t$ から $V$ に変わる置換積分となっているため,やや高度な計算ですが,数学として考えれば大した計算ではないでしょう。
あるいは先に,$\varDelta q=I\varDelta t$ の関係式から,(2)を用いて,$$\varDelta q=\bun{m}{B^2d^2}\varDelta V$$として $\varDelta q$ と $\varDelta V$ の関係式を求めてしまっても良いでしょう。
いずれにしても,次の設問に繋がる内容なので,少し時間をかけてでも正解にたどり着きたい設問。
Ⅰ(4)
起電力に逆らって電荷を運ぶ際の仕事を求める内容です。電圧が $V$ のとき,$\varDelta q$ の電荷を運ぶ際に必要な仕事は,$\varDelta W=V\varDelta q$ と表せます。
求める仕事はこれの足し合わせですので,$$W=\int_0^{Q}Vdq$$を考えればokです。$$\varDelta q=\bun{m}{B^2d^2}\varDelta V$$なので,
$$\begin{aligned}W&=\int_0^{Q}Vdq\\&=\int_0^{V_0}\bun{mV}{B^2d^2}dV\\&=\bun{m}{B^2d^2}\int_0^{V_0}VdV\\&=\bun12\cdot\bun{mV_0}{B^2d^2}\cdot V_0\\&=\bun12QV_0\end{aligned}$$
と計算できます。

まともに考えるとちょっと大変。そこで問題文をよく読んでみると…。
問題文がやたらと長く,「コンデンサーを充電する際の電流や電気量と電圧の関係と同じ」という誘導がなされていることに気づけるとなお良いでしょう。
これってつまり,「$Q=CV$ みたいな式になってますよね?」と言ってくれているのです。
(3)の答えをみると確かに,$$Q=\bun{m}{B^2d^2}V_0$$となっていて,$C=\bun{m}{B^2d^2}$ とみなせば $Q=CV_0$ です。
ということで,誘導を踏まえると,「エネルギーもコンデンサーと同じく,$\bun12CV_0\!^2=\bun12QV_0$ とかけるはず!」ということがわかるのです。
"空気が読めれば",$W=\bun12QV_0$ であることが一瞬で分かるわけですね。

長い問題文をみると嫌な気持ちになるかもしれませんが,作問者としては親切のつもりなのです。丁寧に誘導を読み解きましょう。
Ⅰ(5)
まともに計算すれば,ジュール熱が$$QV_0-\bun12QV_0$$と計算できるのですが,こちらも誘導を踏まえて解けるとより良いでしょう。
誘導によると,コンデンサーの充電と同じように考えられるということでしたよね。つまり,以下のような回路と同じようなことを考えているに過ぎないわけです。
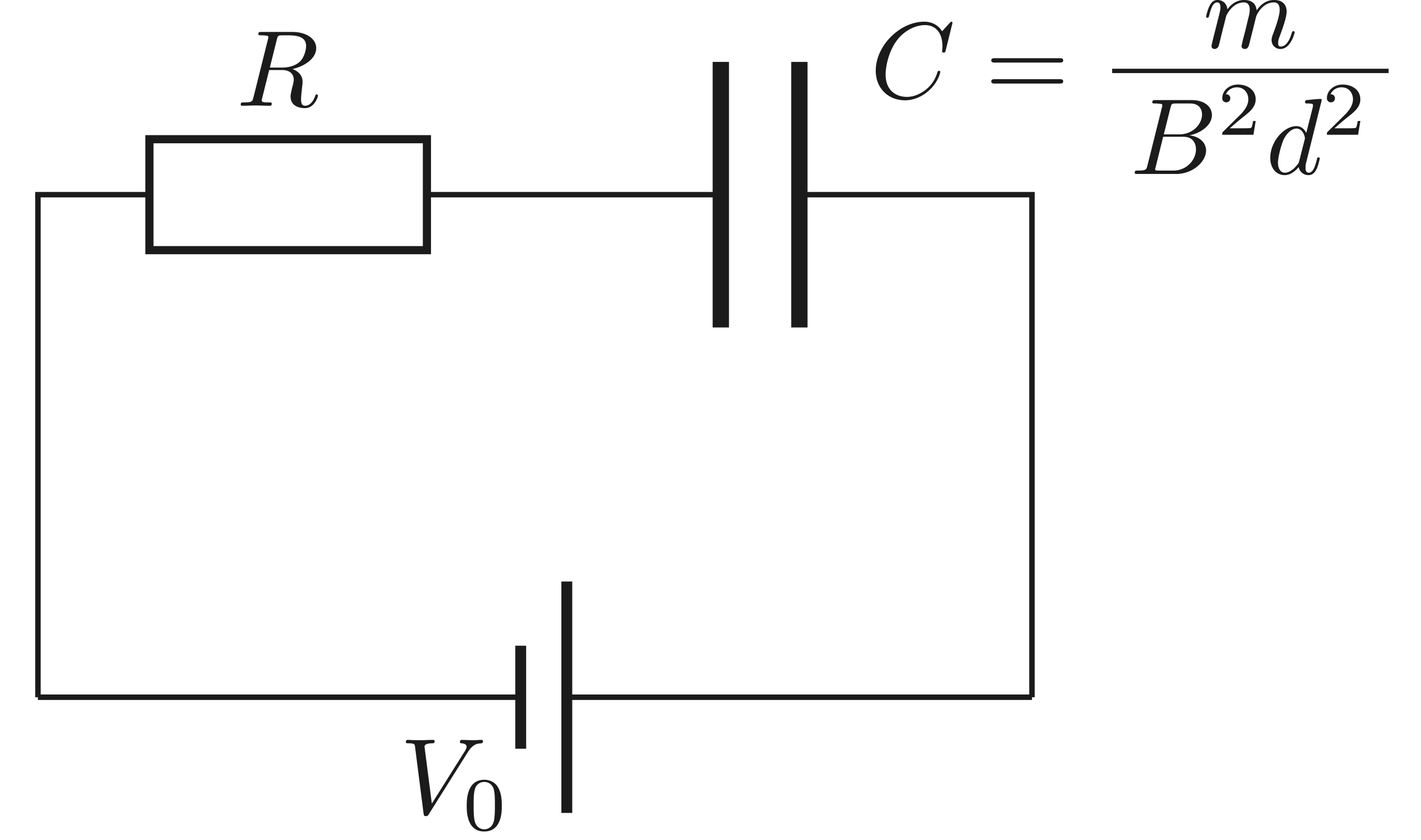
問題演習を十分に積んできている人であれば,「電池の仕事 $QV_0$ のうち,半分がジュール熱,半分がコンデンサーのエネルギー」ということはすぐにわかるでしょう。
今回の設問もこれと全く同じであることを踏まえると,すぐに答えが出せてしまいます。
逆に,この(5)の性質を利用して(4)を解くという手法もありかと思います。なにも前の問題から順番に解く必要はないのです。後ろの問題の答えがわかってしまえば,そこから逆算するのも立派な戦略です。
上記の話が理解できて,スムーズに回答できるのが理想ですが,「まぁ半分がきっとジュール熱なんだろう…」という「直感」は働くと思いますので,ひとまず書いておいて部分点を狙うのが吉。
Ⅱ
スイッチを入れたままの場合であれば,Ⅰと状況が同じですので,$d\to2d$ とすればokです。
スイッチを開いた場合は回路に電流が流れず,導体棒に働く電磁力の大きさも $0$ になるため,速さは変わらないということに気付きたい。
よくわからなくても,時間がなくても,空欄で出すのは御法度です。

全くわからなくても,どんな手を使っても1点でも多く取るという姿勢が大切。
$d$ が $2$ 倍になっているだけですから,ひとまずⅠ(1)の答えをみて,「起電力は $V_0$ だから $d$ 関係なし,$s_0$ は分母に $d$ があるから $\bun12$ 倍!」くらいならすぐにわかると思いますので,ひとまず「カ」と「ク」を $1$,「キ」と「ケ」を $\bun12$ としておくのがよいでしょう。
これで半分は絶対に合っているはずですよね。
それすらわからなくても,$d$ を $2$ 倍しているだけですので,空欄に入るのは $1$ ,$2$ ,$\bun12$ のどれかだということくらいは予想が付くはずです。後は運に任せて適当に埋めておきましょう。1つか2つくらいは当たるはずです。
Ⅲ
ここまで来ると力尽きている人も多いのでしょうが,やはり基本は「運動方程式」と「キルヒホッフの第二法則」です。

最後の問題でも,基本に忠実に。
キルヒホッフの第二法則を立式すると,「棒の速度の関係式がほしいな…」ということに気づくはず。そして運動方程式を考えると,「質量が同じで,働く力の大きさが常に $1:2$ だから,加速度も常に $1:2$ だ!」とわかるはずです。
「ちゃんとわかっている人」にとっては簡単な問題でしょう。「本当によくわかっている一部の人」と,「それ以外の人」で差のつく問題でしょう。
後者のほうが圧倒的に多数だと思いますので,理Ⅰ・Ⅱであれば解けなくても合否には直結しないはずです。解ければ大きなアドバンテージになるでしょう。
こういう問題を時間をかけずに解けるようになりたいものです。
第3問
手書き解答
東大2020_3Ⅰ(1)について
表を見ながら引き算するだけなので答えのみ記した。
前半の問題で配点も高いと思われるため,後半の問題が解けそうにない場合,本問の答えに自信がない場合など,確実に部分点を押さえておきたい場合には途中経過も記載すべき。
Ⅱ(3)について
気体Xについても,内部エネルギー変化が $\varDelta D\SUB{Y}$ であることに言及すれば部分点がもらえる可能性もある。
ただし,記述がやや長くなるため,解答に自信があればエネルギー保存則の立式のみでも可。
全体として
本問のように,気体の状態変化の組み合わせを考える問題では,以下の定石を落ち着いて思い出しましょう。
状態変化の問題へのアプローチ
「定積変化」「定圧変化」「等温変化」「断熱変化」の組み合わせをまずは疑う。
どれにも当てはまらなければ,「$P-V$ グラフが直線になる変化」「真空への断熱自由膨張」を考える。
基本的に,9割以上の問題が「定積変化」「定圧変化」「等温変化」「断熱変化」の組み合わせ です。

本問のように一見複雑そうにみえる問題でも,「どうせ4つの組み合わせだろう」と疑ってかかることが大切。
今回の問題は,定圧変化と断熱変化の組み合わせになっていますね。操作①,③が断熱変化,操作②,④が定圧変化です。
まずはこのことをしっかりと認識することが大切です。
断熱変化の部分ではポアソンの法則を用いて考えることが多いですが,今回の問題では表で情報が与えられているため,ポアソンの法則を使う必要はありません。
余裕があれば,操作①,③の前後で$$PV^{\gamma}=\stext{(一定)}$$となっていることを確認しておきましょう。
Ⅰ
操作①と③は断熱変化なので $W^{in}=\varDelta U$ から,操作②は定圧変化なので,$P-V$ グラフの面積から $W^{in}$ を求めればokです。
記述し始めるときりがないので,答えに自信があれば答えのみでよいでしょう。それ以降の問題が解けなくて,ここで確実に点数を取っておきたい際には途中経過も簡潔に書くとよいと思います。
Ⅱ(1)
計算問題。絶対に失点してはいけない問題です。
Ⅱ(2)
操作④が定圧変化であることに注目しましょう。単原子分子理想気体の定圧変化では,$$Q^{in}:\varDelta U:W^{out}=5:3:2$$が成立します。
この「比の関係式」が使えるのと使えないのとでは問題の難易度が大きく変わることもあるので,定圧変化をみたら必ず思い出しましょう。
定圧変化のエネルギー収支
単原子分子理想気体の定圧変化では,$$Q^{in}:\varDelta U:W^{out}=5:3:2$$が成立する。
(1)で,$W^{in}$ を求めていますので,これを $-\bun32$ 倍すればすぐに答えが求まります。
いずれにしても答えは求まるはずですので,「いかに時間をかけずに答えを出すか」が大事です。
Ⅱ (3)
まずは定圧変化として,$$Q^{in}=-\bun52W^{in}$$から考え始めます。
今回求めるのは $T\SUB{E}$ ですので,操作④で容器X内の気体が受け取る熱量 $Q^{in}$ を別の形で求める必要があります。
操作④で気体Xに熱を与えているのは容器Y内の気体であり,気体Yにおける熱力学第一法則から,$$Q^{in}=\bun32R(T_{\mathrm{E}}-T_{\mathrm{D}})$$であることがわかりますね。
これらを組み合わせて,$$\bun32R(T_{\mathrm{E}}-T_{\mathrm{D}})=-\bun52W^{in}$$を $T_{\mathrm{E}}$ について整理すればokです。
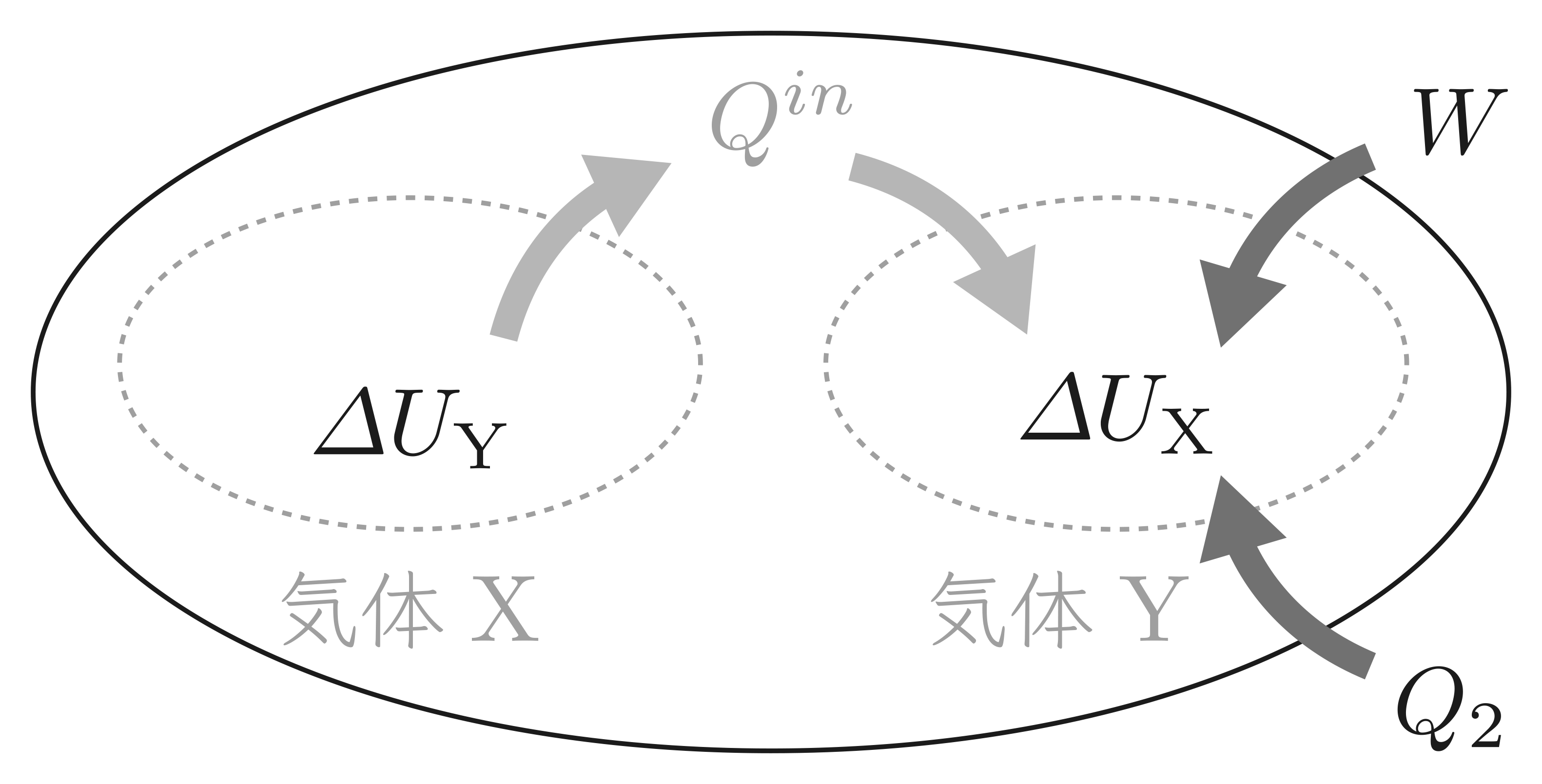
なお,エネルギーの流れを図で表すと以下の通りです。
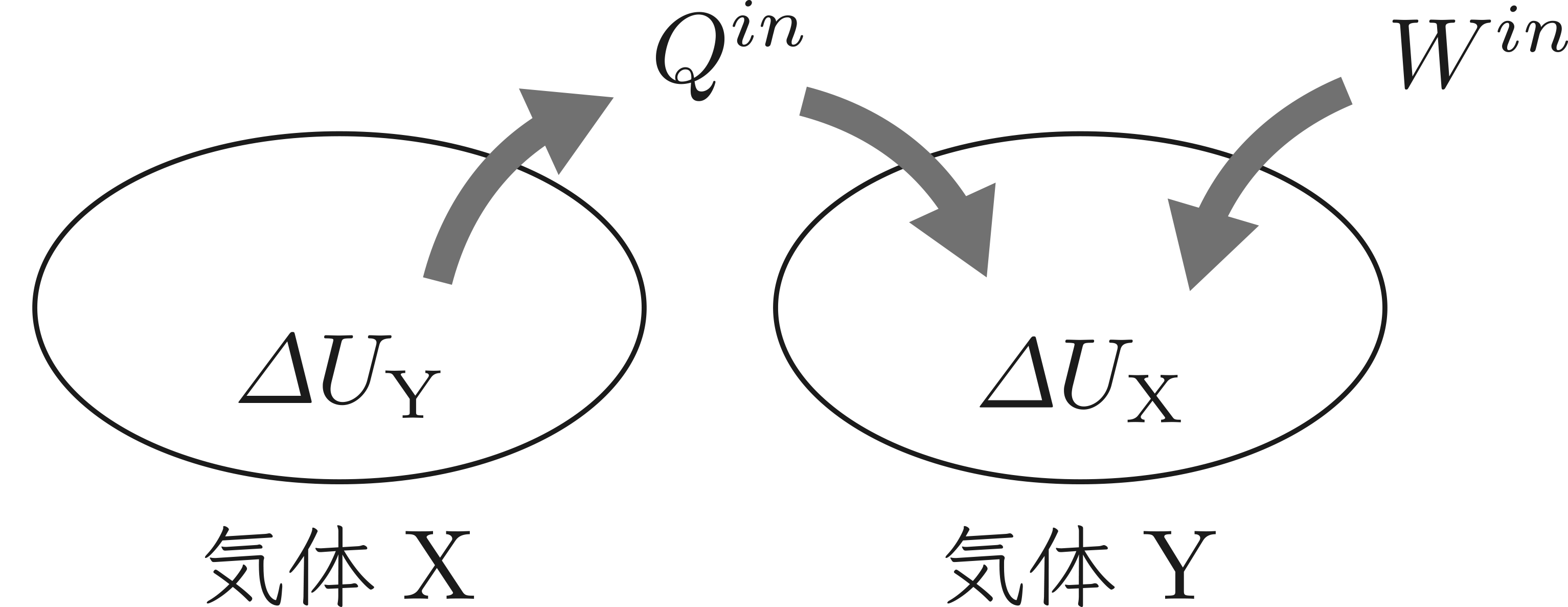
なお,気体Xと気体Yをまとめて1つの系とみなした場合,図は以下のように整理できます。
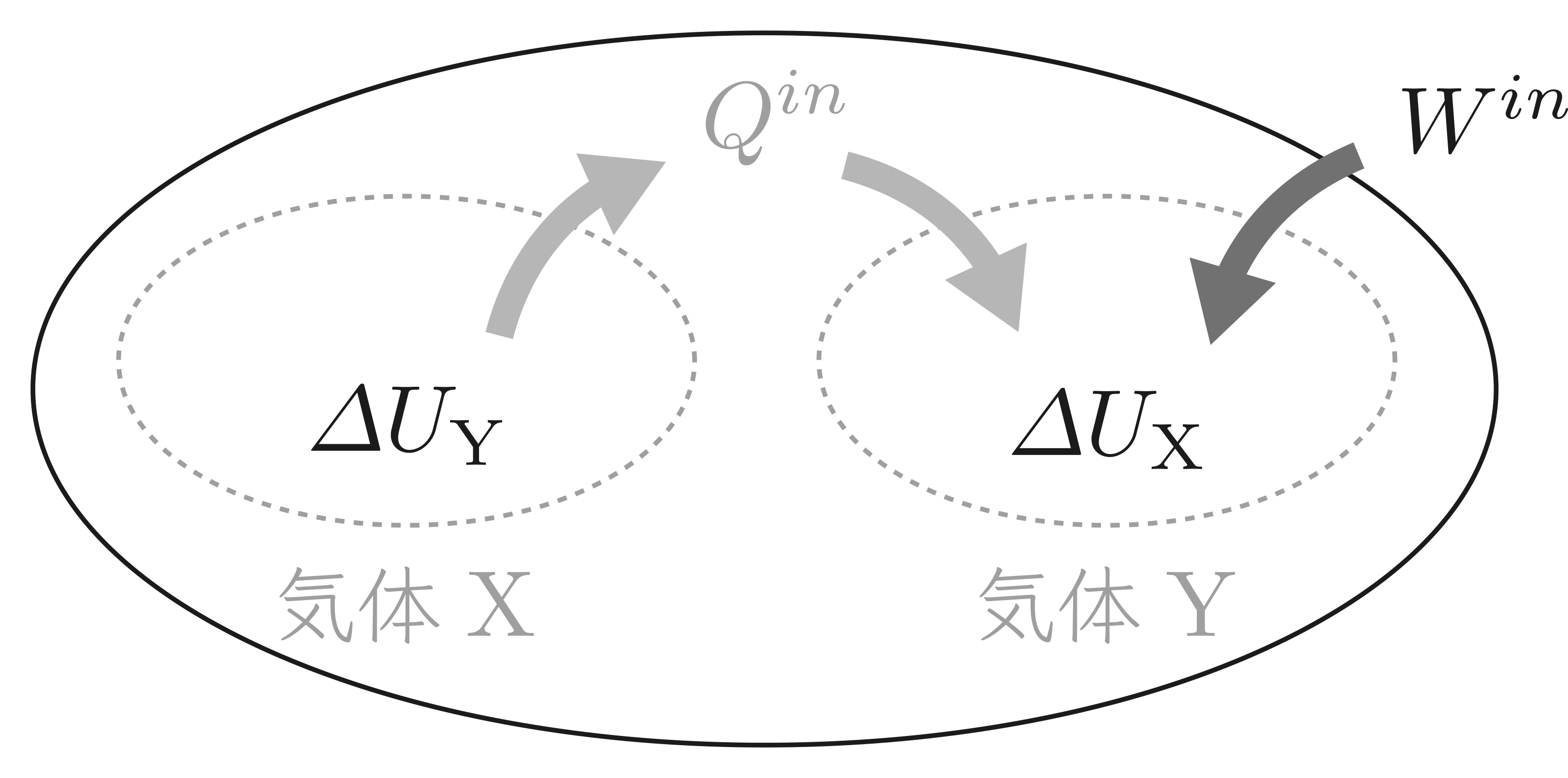
2つの気体をまとめて全体とみなしているので,気体Xと気体Yの間の熱のやり取りは「内部での熱の移動」として捉えることができます。
外部から流入しているのは $W^{in}=W_4$ のみであり,この仕事によって内部エネルギーの和 $\varDelta U_{\mathrm{Y}}+\varDelta U_{\mathrm{X}}$ が変化します。
これを式で表現すると,$$\varDelta U_{\mathrm{Y}}+\varDelta U_{\mathrm{X}}=W_4$$になりますね。
これが系全体でのエネルギー保存則になります。
系全体でのエネルギー保存
エネルギーの流れを表す図をかいて考える。
この「系全体でのエネルギー保存」を考えるのが苦手な人が非常に多いため,本問は差が付きやすい問題といえるでしょう。
Ⅱ(1)
まず,今回の問題では「気体Xが物体Zから熱を受け取り,気体Yに熱を運んでいる」という流れを読み解くことが大切になります。
そのためにまずは,「物体Zがなかったら」という状態を考えてみましょう。この状態であれば,容器Xが動いたり,おもりの量が変わったりするのを繰り返すだけで,操作④において気体Xと気体Yの間での熱のやり取りはないはずです。
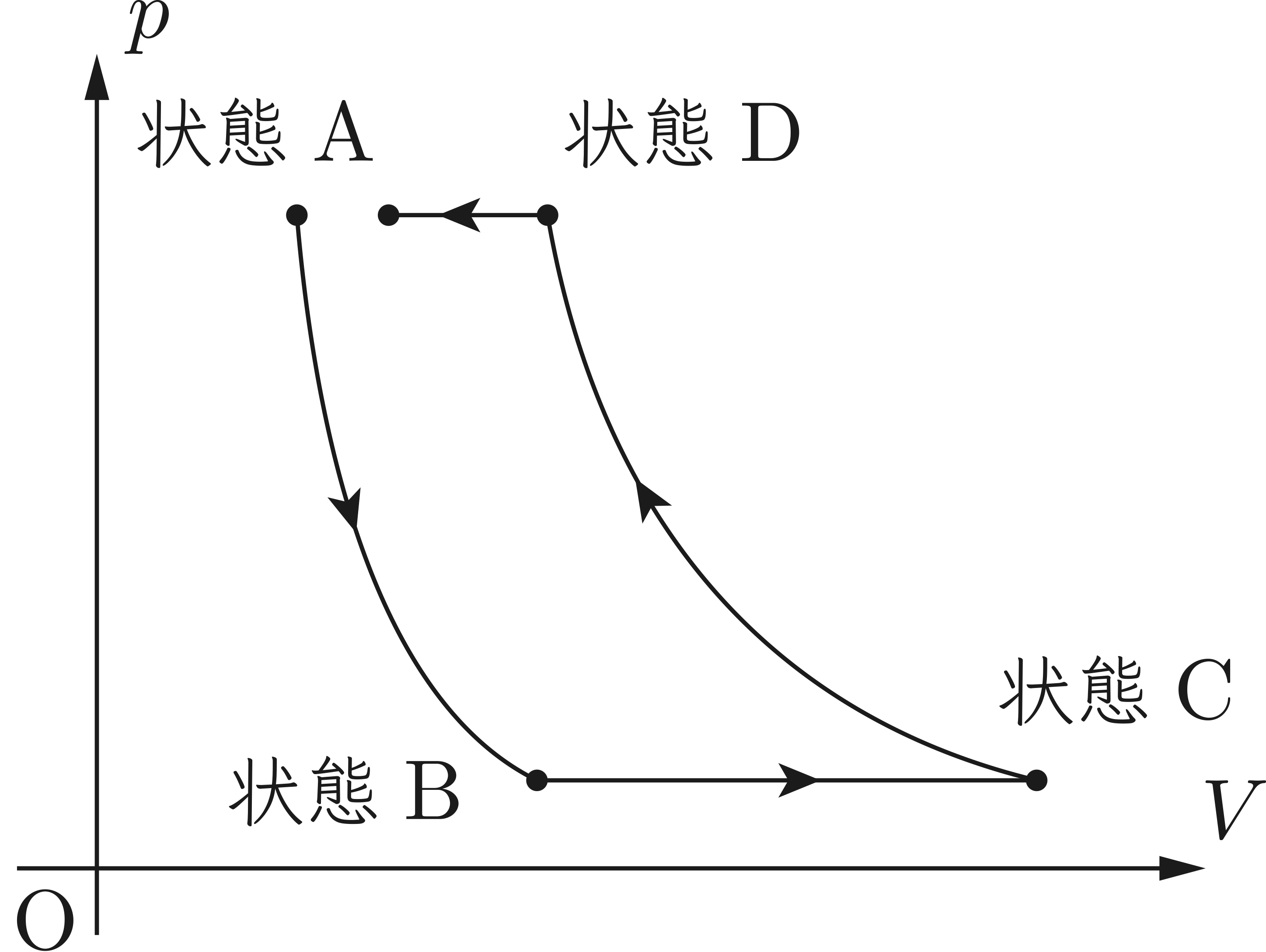
気体Xは断熱変化を繰り返すだけですので,$P-V$ グラフは以下の通りです。気体Xは全く同じ状態を行き来します。

では,操作④で気体Xが気体Yに熱を受け渡すために必要な条件は,と考えると,「操作②で,物体Zから気体Xが熱を受け取る」ことだとわかります。
操作②は定圧変化ですので,$$\stext{(熱を受け取る)}\Leftrightarrow\stext{(体積が増える)}$$ということになります。
この条件が満たされれば,操作④において気体Xから気体Yへと熱が受け渡されることになります。
操作④は定圧変化であり,気体Xの体積は小さくなりますが,状態Aまでは戻らないことを踏まえると,解答の $P-V$ グラフが選べるわけです。
そこまでよくわからなくても,
- 操作①,③が断熱変化,操作②,④が定圧変化
- 状態Aよりも状態Dの温度のほうが高い
ことがわかっていれば「ウ」と「オ」に絞れますし,そこからどちらかを選べといわれたらなんとなくでも「オ」が選べるのではないでしょうか。
しっかりと理解しきって選ぶとなると難しいですが,とりあえず答えを選ぶという意味では難しくないものと思われます。
ちょうど差がつきやすい問題といえるため,なんとか正解の選択肢にたどり着きたいところです。
Ⅲ(2)
以下のどれかが考えられればokです。
- 状態Eよりも状態Dの温度のほうが高い
- 操作②で,気体Xの体積が増える(温度が上昇する)
前者で考えるのであれば,$T_{\mathrm{E}}$ を直接求めることになりますし,後者なら表からすぐに答えが出せます。
$T_{\mathrm{E}}$ を求め間違えていても本問の答えが確実に合うように,後者の方法で,$$a^3\bun{RT_{\mathrm{A}}}{p\SUB{A}}<\bun45a^5\bun{RT_{\mathrm{A}}}{p\SUB{A}}$$と立式するのが懸命でしょう。
間違いが連鎖しないような方法を選択することはとても大切です。
Ⅲ(3)
与えられている仕事が操作①〜④の合計になっていますので,操作全体で見た際のエネルギー保存則を考える,という方針にはすぐに至るでしょう。
$\varDelta U_{\mathrm{Y}}$ が気体Yの内部エネルギー変化であることを考えると,気体X,気体Y単体ではなく,両気体を合わせた系全体でのエネルギー保存を考えないといけない,という点もわかりやすいかと思います。
図をかいて状況を整理すると以下の通りです。
この図から,$$\varDelta U_{\mathrm{X}}+\varDelta U_{\mathrm{Y}}=W+Q_2$$であることがわかりますが,問題は $\varDelta U_{\mathrm{X}}$ ですね。
気体Xについて考えると,状態A(温度 $T_{\mathrm{A}}$)から状態E(温度 $T_{\mathrm{E}}$)へと変化しているわけですが,この温度変化が実は気体Yと同じであることがわかります。
すると,物質量も等しいので,$\varDelta U_{\mathrm{X}}=\varDelta U_{\mathrm{Y}}$ であることに気づけますね。この点に気付けるかが勝負でしょう。
エネルギー保存則を系全体で立式して,かつ $\varDelta U_{\mathrm{X}}=\varDelta U_{\mathrm{Y}}$ を見抜かないといけないので難易度としてはかなり高めです。
解けなくても合否には直結しないでしょう。
Ⅲ(4)
繰り返すとどうなるかを考える問題ですが,まずは2周目を考えてみましょう。
状態Eからスタートし,断熱変化によって圧力が $\bun{p\SUB{A}}{a^5}$ の点に至り,そこから定圧変化になります。
さて,定圧変化(操作②)が終わった後,気体Xの温度はいくらになるでしょう。
物体Zと気体Xの温度が等しくなったところで操作②が終わるわけですから,$\bun45T_{\mathrm{A}}$ ですね。つまり,状態Cに再度至るわけです。
続く操作③は断熱変化ですが,始まりが状態Cですので,終わりも状態Dと一致します。
そして操作④で気体Yに熱を与えることになりますが,1周目と比べると気体Yの温度が高くなっているため,気体Xが気体Yに与える熱量は少ないことがわかります。
よって,体積の縮小具合も小さくなるため,状態Eよりも体積が大きな点で操作④が終わりますね。
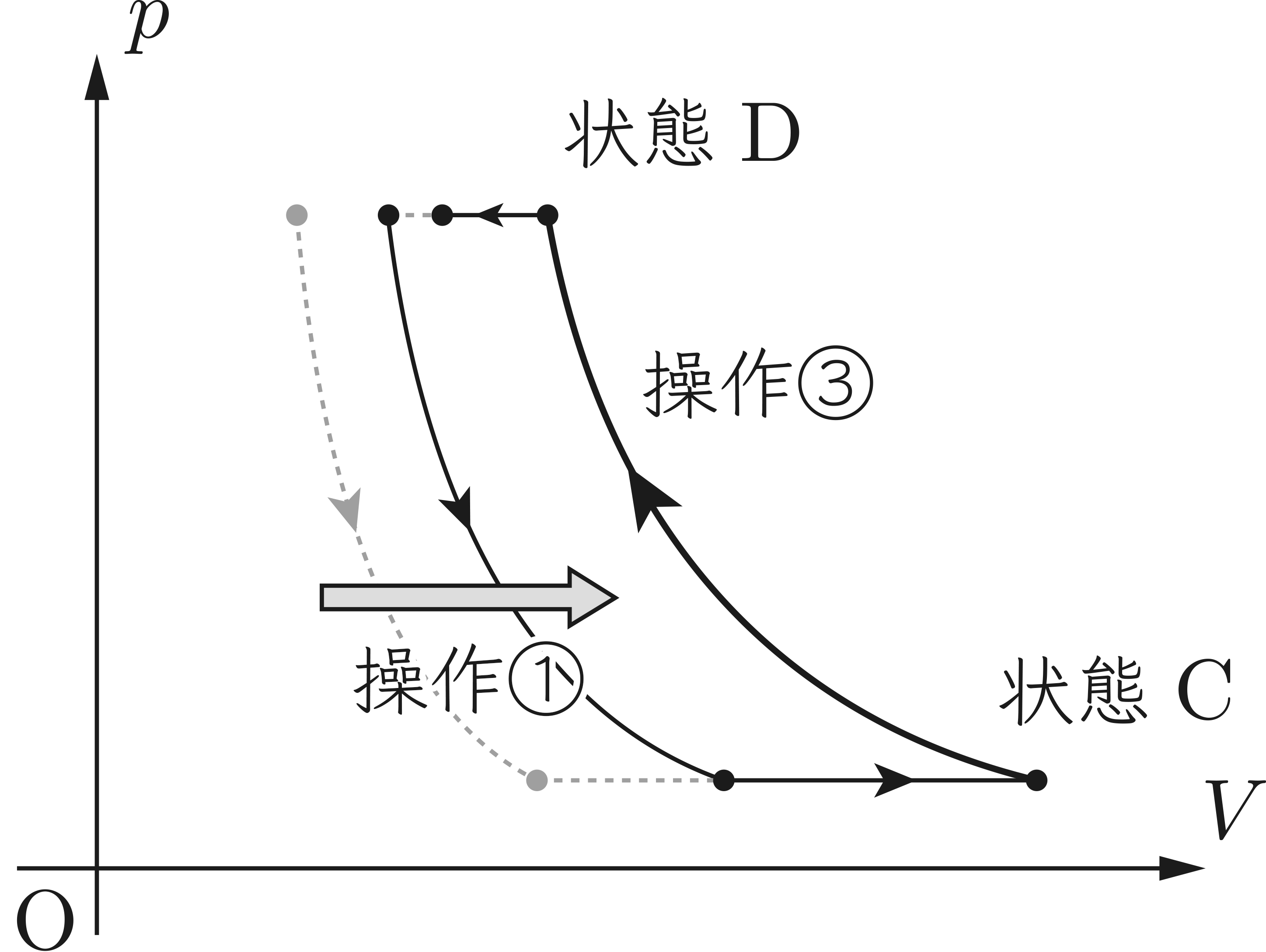
図に太線で示したように,何度繰り返しても操作③のスタート地点は状態C,ゴール地点は状態Dです。
一方で,操作①の断熱変化の $P-V$ グラフはだんだんと右へ寄っていき,最終的に操作③の断熱変化のグラフと重なることが予想されます。
この状態に至ると,
- 操作②で,気体Xに変化が起こらない(温度も体積もそのまま)
- 操作④で,気体Xに変化が起こらない(温度も体積もそのまま)
という状況になりますね。
前者で考える場合,最終的に操作①の前の温度(状態Aに対応)が $T_{\mathrm{F}}$,操作①の後の温度(状態Bに対応)が $\bun{T_{\mathrm{F}}}{a^5}$ であることに注意すると,$$\bun{T_{\mathrm{F}}}{a^5}=\bun45T_{\mathrm{A}}$$と立式できます。
一方,後者で考える場合には,$T_{\mathrm{D}}=T_{\mathrm{F}}$ とすればokですので,表から,$$T_{\mathrm{F}}=\bun45a^2T_{\mathrm{A}}$$と速やかに立式できます。
状況の整理ができれば答えはスムーズなのですが,まぁ難しいですね。
$T_{\mathrm{D}}=T_{\mathrm{F}}$ になんとなくでも気付ければ,正解が得られてしまいますが…。


